希尔伯特变换生成IQ信号

背景

笔者最近在做一个小项目，里面有一部分需要做ssb调制，我负责数字信号处理部分，得把语音信号转换成IQ信号输出，用于后续的调制和传输。

传统的IQ信号生成通常需要硬件正交混频器，但在软件无线电架构中，我们可以通过数字信号处理直接生成IQ信号。核心问题是：如何从单路实信号（语音）生成正交的I/Q两路信号？

有一个办法是做 fft，然后直接在负频域对每个点乘以 -1 实现相移，然后 ifft 获得移相后的信号。这个方案有个缺点，板子上需要跑其他任务，fft 有些吃资源了，而且(补充另一个缺点)

希尔伯特变换提供了一个优雅的解决方案：通过对实信号进行90度相移，可以直接生成解析信号（复信号），其实部和虚部就是I和Q分量。

希尔伯特变换原理

对于实信号 s(t)，做希尔伯特变换本质是将其与 1/(πt) 进行卷积： s̃(t) = s(t) * 1/(πt) 实质上是对信号的所有信号加一个90读的相移，最终得到解析信号，也就是 IQ： $$ z(t) = s(t) + j·s̃(t) \\ z(t) = I(t) + j·Q(t) $$ 也得到了解析信号，也就是 IQ。可以直接扔给dac，进而输出给射频前端进行调制。

当然，对于PSK等相位调制，也可以计算其相位突变进行解调。

对于语音信号（典型带宽300Hz-3400Hz），希尔伯特变换可以很好地生成正交分量，满足IQ输出的需求。

仿真

以音频经典16Khz采样率为例，在matlab中弄了一个100阶，通带归一化频率为 0.01-0.99 的希尔伯特变换器：

希尔伯特变换器

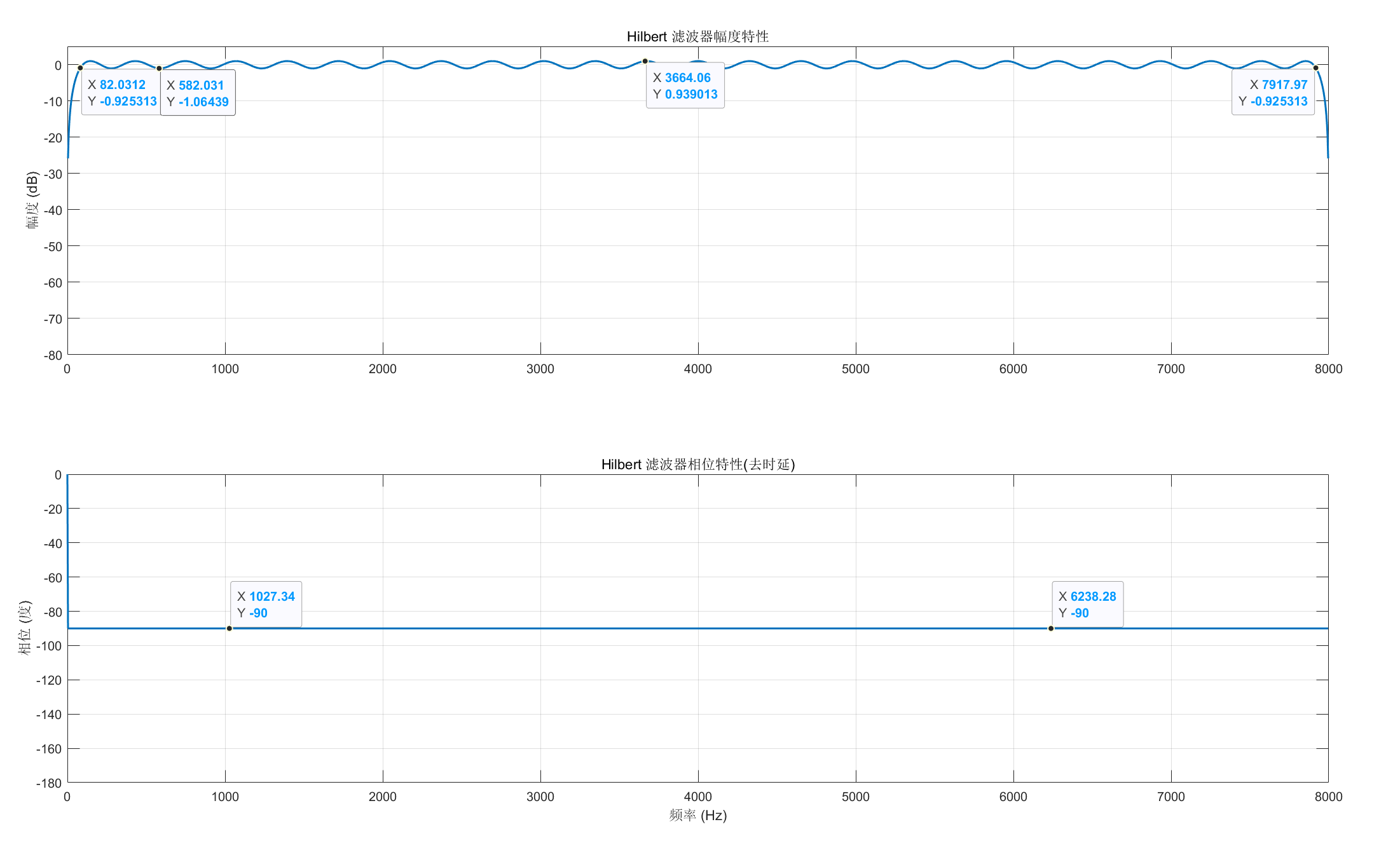
实际通带大概在 80Hz-7.9KHz，带内波动1dB，基本可以接收，移相稳定在-90度。

给两个频率的信号进去看一下相位差：

1Khz/2Khz IQ信号补偿群延迟

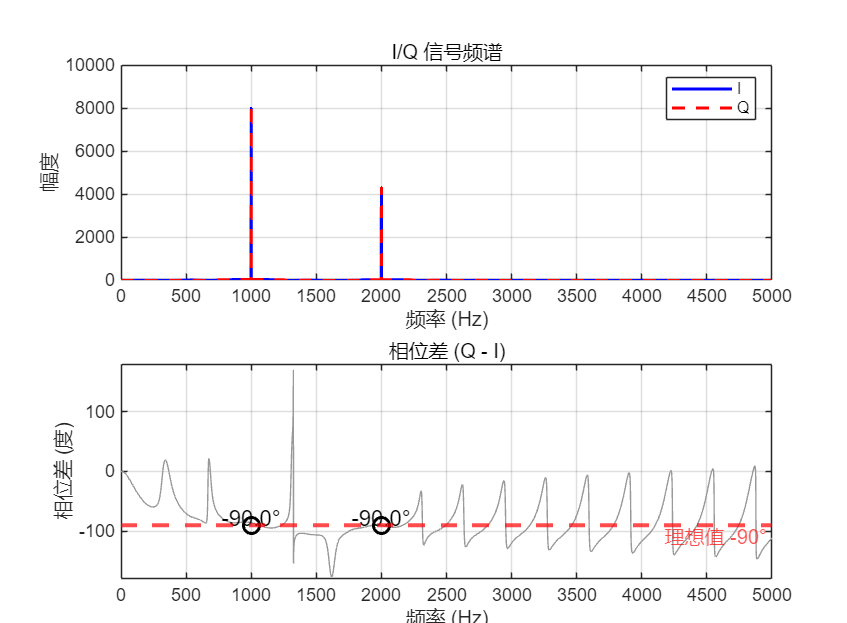
效果也挺好，1KHZ和2KHz位置相位差都是-90度，幅度基本一致。注意，这里对Q路信号的群延迟进行了补偿，I路挂了一个全通滤波器。我们看看不接滤波器有没有什么影响：

1Khz/2Khz IQ信号不补偿群延迟

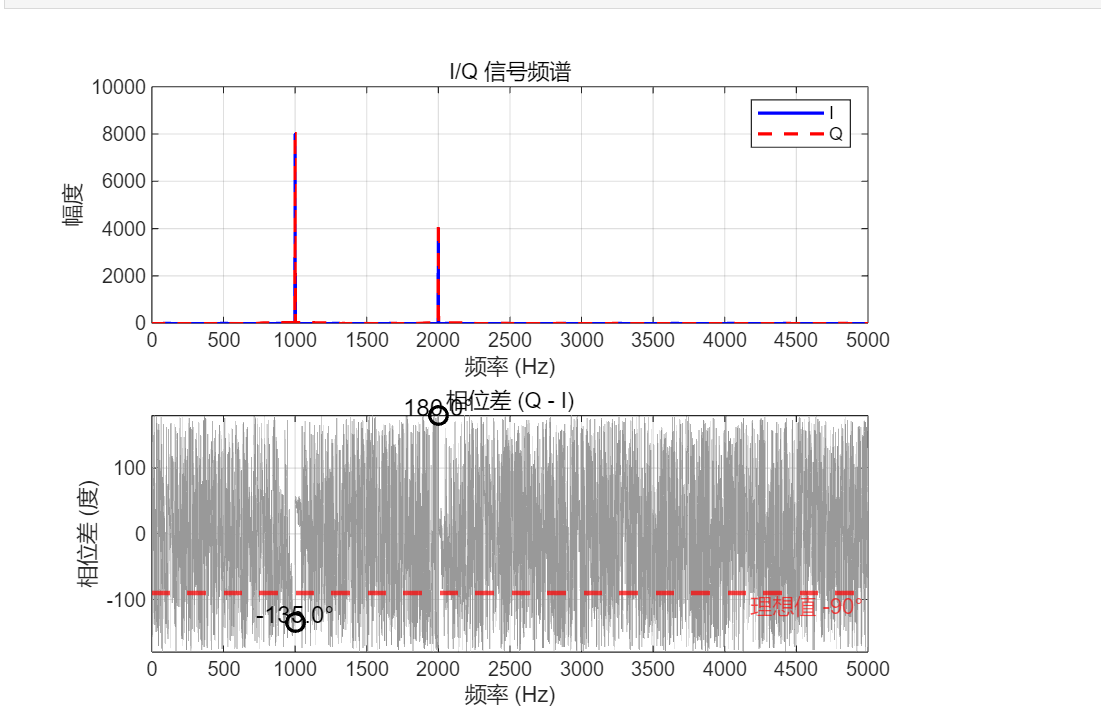
幅度没什么变化，相位已经炸了，为什么呢？分析一下原因：

对于一个线性相位 FIR 滤波器，群延迟是一个固定的时间延迟 τ，表示信号通过滤波器后的时间偏移。

对于 N 阶 采样率为 F_s 的FIR 滤波器，其群延迟为： $$ \tau = \frac{N}{2 \cdot F_s} $$ 固定的时间延迟 τ 在频率 f 处产生的相位延迟为： $$ \phi(f) = -2\pi f \cdot \tau = -2\pi f \cdot \frac{N}{2 \cdot F_s} $$ 也就是相位延迟与频率成正比，频率越高，相位延迟越大。

对于N 阶希尔伯特变换器而言，理想频率响应为 H_Hilbert(f) = −j ⋅ sign(f) ⋅ e^−j2πfτ 相位分解为两部分：

1. Hilbert 相移：-90°（对应 −j）
2. 群延迟相移：$-2\pi f \cdot \frac{N}{2 \cdot F_s}$

那么输出Q路信号的总相位为： $$ \phi_Q(f) = -90° - 2\pi f \cdot \frac{N}{2 \cdot F_s} $$ 如果能在I路加一个N阶段的全通FIR，补偿$-2\pi f \cdot \frac{N}{2 \cdot F_s}$这一部分的理想相位延迟，就能让所有通带各个频率的相位延迟为 -90 度。 $$ \Delta\phi(f) = \phi_Q(f) - \phi_I(f) = \left(-90° - 2\pi f \cdot \frac{N}{2 \cdot F_s}\right) - \left(-2\pi f \cdot \frac{N}{2 \cdot F_s}\right) = -90° $$ 构成了理想希尔伯特变换器。

如果不补偿群延迟的话，计算一下F_s为16KHz，N为100，频率分别为1Khz和2Khz的相位：

Fs = 16000;
N = 100;
tau_delay = N/2 / Fs;  

f_test = [1000, 2000];

phase_I = -2*pi * f_test * tau_delay * 180/pi; 
phase_Q = -90 - 2*pi * f_test * tau_delay * 180/pi;

theory_diff = phase_Q - phase_I;
theory_diff = mod(theory_diff + 180, 360) - 180;  % 归一化相位差

phase_I_norm = mod(phase_I + 180, 360) - 180;
phase_Q_norm = mod(phase_Q + 180, 360) - 180;

fprintf('1000 Hz: I相位=%.2f°, Q相位=%.2f°, 差值=%.2f°\n', ...
    phase_I_norm(1), phase_Q_norm(1), theory_diff(1));
fprintf('2000 Hz: I相位=%.2f°, Q相位=%.2f°, 差值=%.2f°\n', ...
    phase_I_norm(2), phase_Q_norm(2), theory_diff(2));

群延迟仿真输出

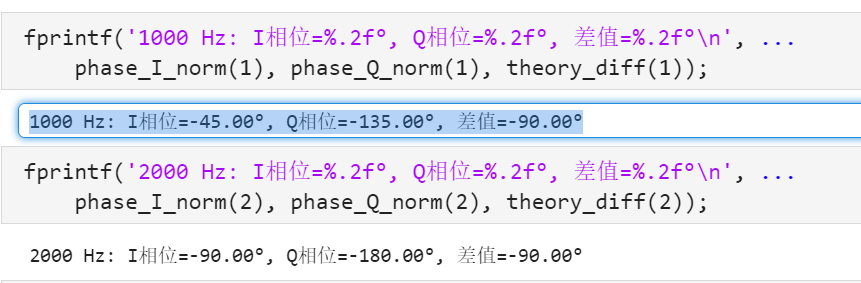
嗯，和之前希尔伯特变换器不补偿群延迟的仿真对上了，说明理论没问题。